Hyperparameter Tuning With Bayesian Optimization
First thing first we need to learn about the Gaussian processes and bayesian optimization.
Gaussian Process
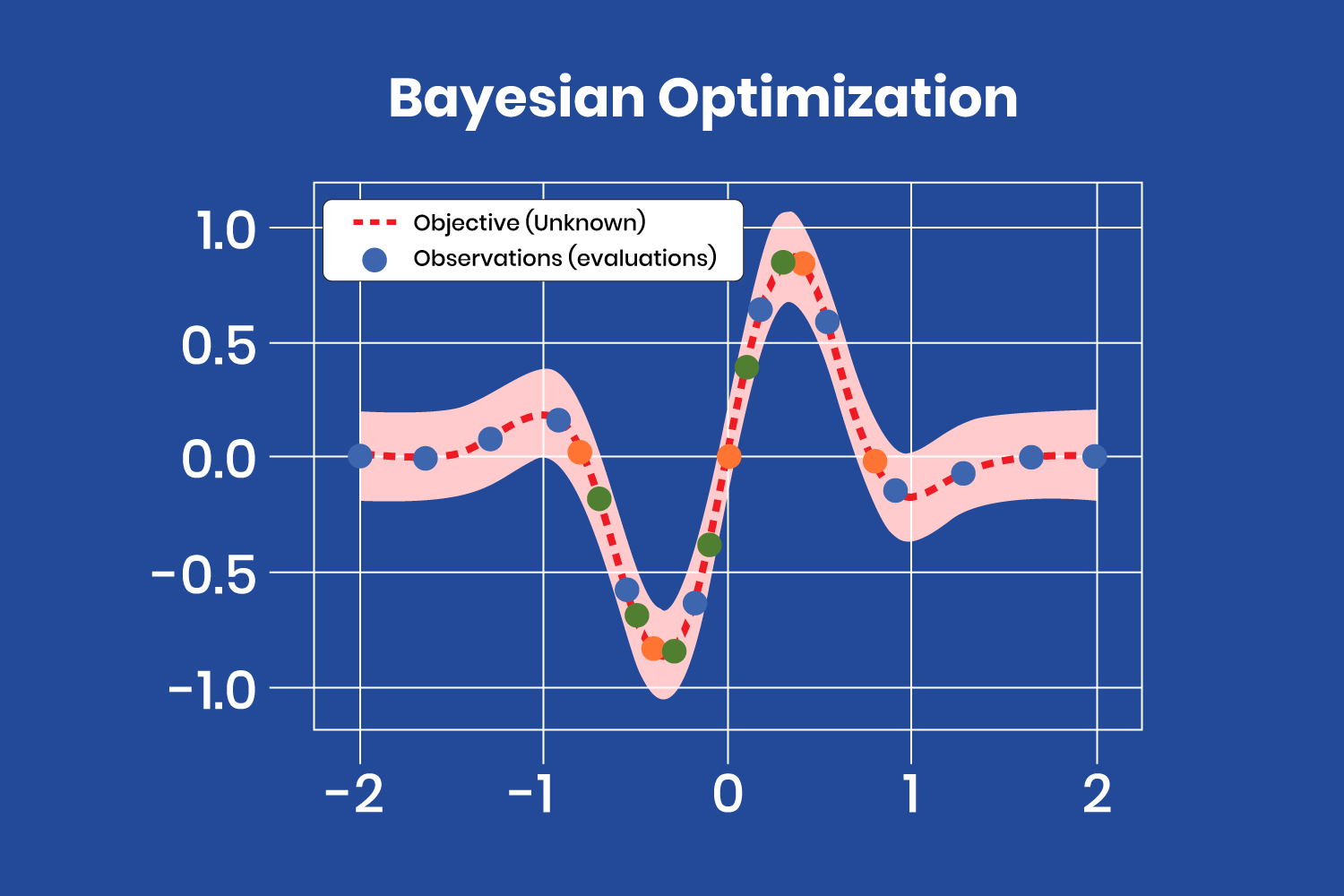
Gaussian processes are a popular and very interesting method for fitting functions, instead of the usual gradient based methods, GPs bring a probalistic way of optimizing: we build an infinite dimensional multivariate normal distribution to represent the function we wish to predict.

This is obviously a generalization, we don’t actually need to represent infinite dimensions but we just need the equation to represent any dimension (x) any time we need it: this is the inference step.
Each point in our predicted function is the mean of P(X|x) (the multivariate normal distribution X given the value x) and the credible region is the variance, on one side it’s sigma**2 on the other it is -sigma**2 it represents the uncertainy of our prediction.
As we can see GP are extremely powerful but there’s assumptions we need to have about our black box function to have for it work:
- Our black-box function needs to expensive to evaluate: gaussian processes thrive in low data environment
- The target function needs to be smooth
Bayesian Optimization
As the name suggests we use bayes theorem: we update our prior belief (prior) with it’s likelihood and the new evidence to obtain our new belief (Posterior), and as you might have figured out we use Gaussian processes!

In bayesian optimization we seek to build a representation of our function to get the maximum/minimum value of it, we of course model this function using GPs! but how do we determine which are the best points to sample to use our Gaussian process with?
We use an acuisition function, it deals with the exploration exploitation tradeoff:
- Exploration meaning getting the values with the most uncertainty (higher variance)
- Exploitation which basically is picking the point with the max/min value (max/min mean)
after we find the next x, we sample it through our function and update the Gaussian Process, we repeat this process until we reached the maximum number of iterations or the acquisition function propesed a point we already sampled (in a noiseless environment).
Hyper Parameter tuning
Model selection
For this article i’m using Random forests through the sklearn library,
from sklearn.ensembles import RandomForestRegressor
def create_model(params: list) -> RandomForestRegressor:
"""
Create a random forest Regressor model
args:
params: parameters for the random forest model
[
0: n_estimators: number of trees
1: max_depth: max depth of trees
2: max_features: max number of features to consider when split
3: max_samples: the number of samples from X to each tree
4: max_leaf_nodes: build with the maximum leaf nodes number
]
Returns:
Model: model to fit data with
"""
Model = RandomForestRegressor(
n_estimators=int(params[0]),
max_depth=int(params[1]),
max_features=params[2],
max_samples=params[3],
max_leaf_nodes=int(params[4])
)
return Modelwe also are using the california housing dataset which is a dataset also provided by us through sklearn
from sklearn.datasets import fetch_california_housing
def load_data() -> Tuple[np.ndarray, np.ndarray]:
"""
Load the california housing data and return x, y
https://scikit-learn.org/stable/datasets/real_world.html\
#california-housing-dataset
Returns:
X: features to predict from
Y: target prediction (house price)
"""
data = fetch_california_housing(data_home='./data')
return data['data'], data['target']Hyperparameter selection
We need to select the hyper parameters to tune before optimizing them, in my case i’ve used
n_estimators: number of trees
max_depth: max depth of trees
max_features: max number of features to consider when split
max_samples: the number of samples from X to each tree
max_leaf_nodes: build with the maximum leaf nodes number
In Random forests these are the most important features to tune.
Metric selection
In bayesian optimization it’s best to have a singular value to tune with, since we are doing regression, i’m using mean squared error with cross validation which will split our data into train/valid/test sets for us at each iteration using different combinations.
score = cross_val_score(
Model, X, Y, scoring='neg_mean_squared_error').mean()Conclusion
In conclusion, hyperparameter tuning is an EXTREMELY important subject in ML and is used heavily, bayesian optimization is a sophisticated choice of tuning the hyperparameters but there are other ways like Grid search for example albeit not as effective but easier to implement and parallelize.
My next step is diving deeply in other areas of which Bayesian optimization is used like reinforcement learning.